Benford law（本福特定律）

Posted on by

  1. 定义

    2. 本福特定律，也称为本福德法则，说明一堆从实际生活得出的数据中，以1为首位数字的数的出现机率约为总数的三成，接近期望值1/9的3倍。推广来说，越大的数，以它为首几位的数出现的机率就越低。它可用于检查各种数据是否有造假。

  2. 解释

    3. 一组平均增长的数据开始时，增长得较慢，由最初的数字a增长到另一个数字a + 1起首的数的时间，必然比a + 1起首的数增长到a + 2，需要更多时间，所以出现率就更高了。
    从数数目来说，顺序从1开始数，1,2,3,…,9，从这点终结的话，所有数起首的机会似乎相同，但9之后的两位数10至19，以1起首的数又大大抛离了其他数了。而下一堆9起首的数出现之前，必然会经过一堆以2,3,4,…,8起首的数。若果这样数法有个终结点，以1起首的数的出现率一般都比9大。

  3. 应用

    4. 1972年，Hal Varian提出这个定律来用作检查支持某些公共计划的经济数据有否欺瞒之处。1992年，Mark J. Nigrini便在其博士论文”The Detection of Income Tax Evasion Through an Analysis of Digital Frequencies.”（Ph.D. thesis. Cincinnati, OH: University of Cincinnati, 1992.）提出以它检查是否有伪帐。推而广之，它能用于在会计、金融甚至选举中出现的数据。

  4. 实例

    5. 4.1 以前当协会会长的时候，曾经管理了一年的协会账目。年底结算前，正好看到了有关”本福特定律”的介绍；于是，好奇之下，用手头的协会账目做了一下检验。

    对于账目的第一个数字，结果基本符合定律，而第二位数字明显不符合定律。之所以会这样，可能有一下原因：（1）账目太少（总共只有55条账目）；（2）有一部分账目因为是别人告诉我然后补记的，所以除了数量级是真实的以外，后面的数字基本上都是约数。（3）如果取第二位数字的话，条目由55减少到了45。
    下面这张图是我把账目找出来重新做的图：
    zhangmu

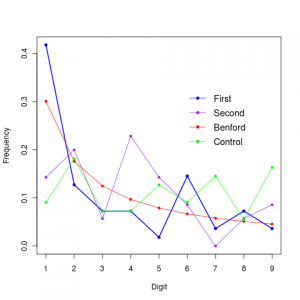
    4.2电脑中文件的大小是否也符合本福特定律呢？

    我把电脑上的所有文件（即根目录下的文件）的大小提取出来，作出了下图：
    benford_1 benford_2
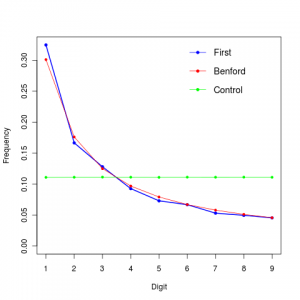
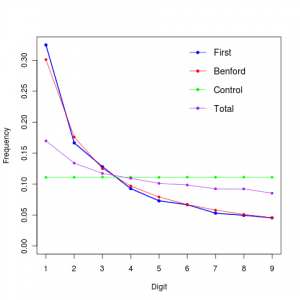
    其中的Total指的是文件大小中数字1-9（不考虑0）出现的频率。
    使用到的代码——获取文件大小，同时产生对照数据（Perl）：

    1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

    #!/usr/bin/perl -W
 
use strict;
use warnings;
use File::Find;
 
my $dir          = $ARGV[0];
my $file_size    = $ARGV[1];
my $file_control = $ARGV[2];
my $num          = 0;
 
open my $OUT, '>', $file_size
or die "$0 : failed to open  input file '$file_size' : $!n";
select $OUT;
 
find( { wanted => &process, no_chdir => 1 }, "$dir" );
 
sub process {
my $file = $File::Find::name;
unless ( -d $file ) {
 
#print "$filet";
my $size = -s $file;
unless ( $size == 0 ) {
$num++;
print "$sizen";
}
}
}
close $OUT or warn "$0 : failed to close input file '$file_size' : $!n";
 
open my $CTL, '>', $file_control
or die "$0 : failed to open  output file '$file_control' : $!n";
select $CTL;
for ( my $i = 0 ; $i < $num ; $i++ ) {
my $random = 1 + int( rand(9) );
print "$randomn";
}
close $CTL or warn "$0 : failed to close output file '$file_control' : $!n";

    统计绘图（R）：

    1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

    filesize <- scan("root_file_size.txt")
filesize.first <- substr(filesize,1,1)
filesize.first.table <- table(filesize.first)
filesize.first.percent <- filesize.first.table/sum(filesize.first.table)
 
number <- 1:9
benford <- log10(1+1/number)
 
false <- scan("false_file_size.txt")
false.first <- substr(false,1,1)
false.first.table <- table(false.first)
false.first.percent <- false.first.table/sum(false.first.table)
control <- as.numeric(false.first.percent)
 
png("benford.png")
plot(filesize.first.percent,col="blue",type="o",pch=20,xlab="",ylab="")
lines(x=number,y=benford,col="red",type="o",pch=20)
lines(x=number,y=control,col="green",type="o",pch=20)
title(xlab="Digit",ylab="Frequency")
legend(6,0.33,"First",col="blue",pch=20,lty=1,bty="n",cex=1.2)
legend(6,0.30,"Benford",col="red",pch=20,lty=1,bty="n",cex=1.2)
legend(6,0.27,"Control",col="green",pch=20,lty=1,bty="n",cex=1.2)
dev.off()

  5. 扩展

    6. 本福特定律（维基百科）
    Benford’s law
    本福特定律（百度百科）
    Benford定律
    Benford定律
    数学真奇妙之benford law

  6. 其他

    7. 齐夫定律